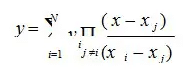Rumus Interpolasi

Rumus Interpolasi Dilengkapi dengan rumusnya akan kami uraikan secara sederhana agar bisa dengan mudah Anda pahami. Untuk pembahasan lebih lanjut, silahkan simak penjelasannya di bawah ini.

Menurut ilmu matemika tentang interpolasi, jika interpolasi digunakan untuk memperkirakan suatu nilai tengah tentang suatu perangkat nilai yang kita ketahui.

Dalam pengertiannya yang lebih luas, bahwa interpolasi merupakan suatu ilmu yang dipakai dalam suatu usaha untuk mendefinisikan mengenai fungsi pendekatan terhadap suatu fungsi analitik yang mana belum di ketahui atau sebuah pengganti suatu fungsi yang rumit yang tidak mungkin untuk didapatkan persamaan analitiknya tersebut.

Yang menjadi masalah umum di dalam interpolasi disini adalah bagaimana caranya bisa menjabarkan fungsi dekatannya. Sedangkan cara atau sebuah metode yang bisa dipakai untuk menyelesaikan masalah dalam interpolasi tersebut disebut metode pinsip subtitusi.

Di dalam mata kuliah juga ada materi yang mempelajari tentang interpolasi yaitu pada mata kuliah metode numerik yang di dalamnya dibagi menjadi dua macam yaitu interpolasi kuadratik dan interpolasi linear, yang mana materi ini dapat kita terapkan di dalam kehidupan kita sehari – hari.

Misal, jika y = f (x) yaitu suatu fungsi terhadap nilai-nilai yakni :

y₀ untuk x₀

y₁ untuk x₁

y₂ untuk x₂

y_n untuk x_n

Bentuk grafiknya adalah:

Maka, jika Φ (x) adalah sebuah fungsi sederhana sembarang dengan sedemikian rupa, maka untuk variable yaitu : x_o, x_i, … …, x_n dapat memberikan suatu nilai yang hampir sama terhadap f (x), jadi jika f (x) akan digantikan dengan Φ (x) pada sebuah interval yang diketahui, hal demikian dapat dikatakan suatu proses interpolasi dan suatu fungsi Φ (x) adalah suatu rumus interpolasi terhadap fungsi.

Suatu fungsi Φ (x) yang dapat dinyatakan ke dalam berbagai bentuk suatu persamaan. Apabila Φ (x) dinyatakan sebauh suatu fungsi polinomial P (x), maka prosesnya disebut dengan interpolasi polinomial atau juga parabolik, sedangkan juga jika Φ (x) ini dinyatakan ke dalam sebuah persamaan fungsi trigonometri, maka proses ini disebut interpolasi trigonometri.

Apabila Φ (x) kita nyatakan ke dalam bentuk fungsi eksponensial, polynomial Legendre atau pun fungsi Bessel atau juga bentuk fungsi spesifik yang lainnya, maka pemilihan tentang bentuk fungsi tersebut bisa didasarkan kepada sebuah anggapan atau perilaku sebuah data yang dapat dianggap cenderung mempunyai suatu pola fungsi-fungsi tersebut.

BACA JUGA:  Panjang Diagonal Persegi Panjang

Pengertian

Interpolasi merupakan suatu teknik mencari harga suatu fungsi pada suatu titik diantara 2 titik yang nilai fungsi pada ke-2 titik tersebut sudah diketahui. Interpolasi sendiri terbagi menjadi beberapa jenis berdasarkan dengan fungsi dan cara penginterpolasiannya.

Rumus

Adapun rumus interpolasi adalah sebagai berikut:

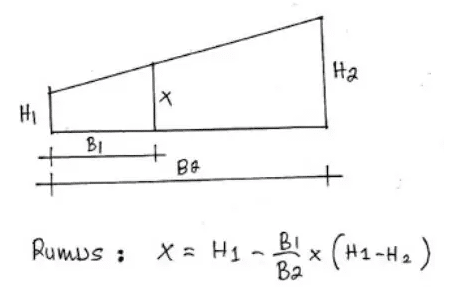
Metode

Interpolasi Linier

Interpolasi linier adalah algoritma matematika yang bisa diterapkan untuk menaksir titik harga tengahan melalui suatu garis lurus pada setiap dua titik masukan yang berurutan. Interpolasi ini adalah polinomial tingkat pertama dan melalui suatu garis lurus pada setiap dua titik masukan yang berurutan. Dua titik masukan itu dipakai untuk menaksir harga-harga tengahan diantara titik-titik data yang sudah tepat. Metode yang paling sering digunakan untuk maksud ini adalah interpolasi polinomial.

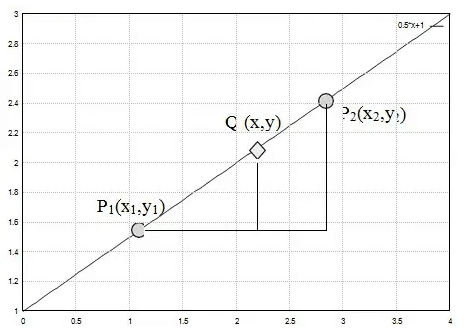
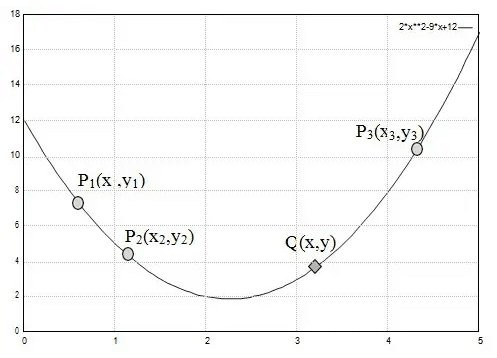
Interpolasi Kuadratik

Interpolasi kuadratik hampir sama dengan interpolasi linier, tapi interpolasi ini memakai berpangkat2 dengan menggunakan 3 titik pada pembentukan sebuah garisnya. Banyak penggunaan interpolasi linier tidak maksimum pada penggunaannya ketika digunakan pada fungsi yang berpangkat dua, sehinggga interpolasi kuadratik ini juga ada agar fungsi dengan pangkat 2 bisa terselesaikan dan bisa dicari titik barunya dengan efektif.

Interpolasi Polinomial

Interpolasi polynomial digunakan untuk mencari titik-titik antara dari n buah titik P₁ (x₁, y₁), P₂ (x₂, y₂), P₃ (x₃, y₃), …, P_N (x_N, y_N) dengan menggunakan pendekatan fungsi polynomial pangkat n-1:

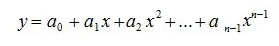
Masukkan nilai dari setiap titik ke dalam persamaan polynomial di atas dan diperoleh persamaan simultan dengan n persamaan dan n variable bebas:

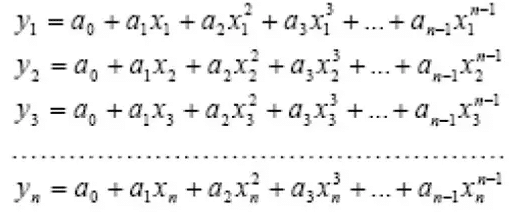
Interpolasi Lagrange

Interpolasi Lagrange merupakan salah satu formula untuk interpolasi berselang tidak sama selain formula interpolasi Newton umum & metoda Aitken. Meskipun demikian bisa dipakai juga untuk interpolasi berselang sama.

Misalnya fungsi y (x) kontinu & diferensiabel sampai turunan (n+1) dalam interval buka (a,b). Diberikan (n+1) titik (x0,y0), (x1,y1), …, (xn,yn) dengan nilai x tidak perlu berjarak sama dengan yang lainnya, dan akan dicari suatu polinom berderajat n. Untuk pemakaian praktis, formula interpolasi Lagrange bisa dinyatakan sebagai berikut :