Pengertian Kubus: Rumus dan Contoh Soal

Pengertian Kubus dilengkapi dengan contoh soalnya akan kami uraikan secara sederhana agar bisa dengan mudah Anda pahami. Untuk pembahasan lebih lanjut, silahkan simak penjelasannya di bawah ini.

Kita pasti menjumpai banyak benda dalam kegiatan sehari-hari. Ada benda yang berbentuk dua dimensi ataupun tiga dimensi.

Ada banyak sekali benda-benda tiga dimensi dalam macam-macam bentuk. Terdapat benda yang bentuknya menyerupai kubus dengan sisi-sisinya berbentuk persegi.

Pada kesempatan kali ini saya akan membahas mengenai bangun ruang kubus, namun sebaiknya kalian mengingat materi mengenai bangun persegi.

Untuk penjelasan yang lebih lengkap, kalian bisa menyimak ulasannya di bawah ini.

Pengertian

Pengertian Kubus adalah Bangun Ruang yang mempunyai bentuk tiga dimensi yang udah dibatasi oleh enam bidang sisi sisinya dan sisi tersebut berbentuk kongruen atau berbentuk bujur sangkar. Kemudian Bangun Ruang ini bisa juga disebut dengan bidang enam beraturan yang berbentuk mirip dengan Prisma Segi empat.

Sedangkan Cara Menghitung Rumus bagun ini biasanya digunakan untuk mengerjakan Soal Matematika yang terdapat di tingkatan sekolah SMP ataupun SMA dan sering muncul juga di soal-soal UN maupun UAS sehingga kaloian harus benar – benar memahami dan tahu tentang Pengertian Kubus serta rumus menghitung luas dan volume Kubus.

Untuk rumus kubus memiliki tiga turunan yaitu Rumus Luas Permukaan Pada Kubus, Rumus Volume Kubus dan Rumus Diagonal Sisi Kubus.

Rusuk Kubus

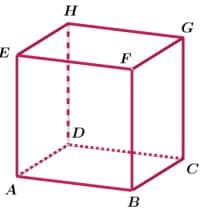
Perhatikan gambar kubus di atas.

Ada berapa banyak jumlah rusuk pada kubus ABCD.EFGH di atas?

• Pada kubus tersebut terdapat 12 rusuk.
• Rusuk-rusuk pada kubus memiliki ukuran yang sama panjang.
• Rusuk AB sejejar dengan rusuk CD, EF, dan GH.
• Rusuk BC sejajar dengan rusuk AD, EH, dan FG.
• Rusuk AE sejajar dengan rusuk BF, CG, dan DH.

Diagonal Kubus

Kubus mempunyai empat diagonal ruang yang menghubungkan dua titik sudut yang berhadapan. Terdapat ruang tersebut antara lain AG, BH, CE, dah DF.

Misalnya panjang rusuk pada kubus tersebut adalah r, maka panjang diagonal ruang kubus yaitu

AC = √(AB² + BC²) = √(r² + r²) = √(2r²) = r √2

AG = √(AC² + CG²) = √((r √2)² + r²) = √(3r²) = r √3

Jadi, panjang diagonal ruang kubus dengan rusuk r adalah r √3.

Diagonal Ruang Kubus

Bidang diagonal pada kubus di atas yaitu bidang diagonal CDEF, ADGF, BCHE, ACGE, dan BFHD. Sehingga terdapat 6 bidang diagonal pada kubus.

Bidang diagonal kubus mempunyai luas yang sama. Misalkan ukuran panjang rusuk kubus adalah r, maka luas bidang diagonalnya (misal bidang diagonal ABGH):

BG = √(BC² + CG²) = √(r² + r²) = √(2r²) = r √2

Luas bidang diagonal = AB x BG

Luas bidang diagonal =  r x r √2 = r² √2

Keterangan:

r  : ukuran panjang rusuk kubus

Rumus

Berikut ini adalah rumus luas dan volume kubus.

Luas

L = 6 × s2

Keterangan :

• L = luas permukaan kubus (cm²)
• s = panjang rusuk kubus (cm)

Volume

V = s3

Keterangan :

• V = volume kubus (cm³)
• s = panjang rusuk kubus (cm)

Contoh Soal

Diketahui sebuah kubus mempunyai panjang rusuk sepanjang 9 cm. Tentukan luas dan volume kubus tersebut Jawab:

Jawab:

Diketahui: 

s = 9cm

Ditanya:

Luas & Volume kubus

Penyelesaian:

L = 6 × s² cm²

L = 6 × 9²

L = 6 × 81

L = 486 cm²

V = s³

V = 9³

V = 729 cm³

Jadi , Luas kubus adalah 486 cm² dan volume kubus adalah 729 cm³