Volume Tabung

Volume Tabung lengkap dengan pengeertian, penjelasan, contoh, rumus dan cara menghitung volume tabung serta gambar nya

Dalam ilmu matematika terdapat beberapa bangun ruang salah satunya iyalah Tabung. Tabung adalah bangun ruang yang dibatasi oleh 2 sisi yang kongruen & sejajar yang berbentuk lingkaran serta sebuah sisi lengkung.

Banyak yang belum mengetahui dengan baik tentang penyelesaian masalah tabung, baik dari Definisi, unsur-unsur & Penentuan Rumus Pada tabung. Penulis membuat makalah yang berjudul “Tabung” untuk memahami lebih jelas lagi tentang Tabung.

Tabung merupakan bangun ruang yang dibatasi oleh 2 bidang yang berbentuk lingkaran sebagai sisi alas & sisi atas & sebuah bidang lengkung yang merupakan sisi tegak yang disebut selimut tabung.

Sifat sifat Tabung

• Memiliki 2 sisi berbentuk lingkaran dan 1 sisi
• berbentuk bidang lengkung (selimut tabung)
• Memiliki 2 rusuk lengkung
• Tidak mempunyai titik sudut

Rumus Volume Tabung

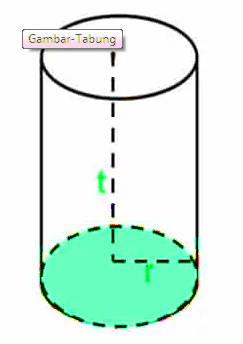
Rumus volume Tabung adalah V = Luas Alas kali Tinggi. Sebelum kita membahas nya, kita perlu memahami apa yang dimaksud dari tabung.

Tabung merupakan bangun ruang tiga dimensi yang memiliki alas & tutup berupa lingkaran yang sama & sejajar serta memiliki selimut berupa persegi panjang yang mengelilingi ke 2 lingkaran tersebut.

Jadi ketika kamu melihat benda-benda seperti kayu yang terpotong, drum, pipa, bambu & benda dengan bentuk yang sama termasuk dalam bentuk tabung.

Bentuk tabung mempunyai ciri yang berbeda dari bentuk lainnya yaitu:

• Mempunyai 2 buah rusuk.
• Mempunyai alas & tutup yang berbentuk lingkaran.
• Mempunyai 3 bidang sisi yaitu alas, tutup & selimut.

Unsur – Unsur Tabung

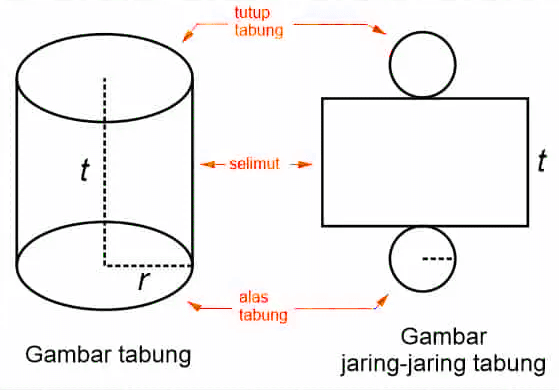
• Sisi tabung

Sisi tabung merupakan bidang yang membentuk tabung. Sisi tabung terdiri dari 2 buah lingkaran & sebuah selimut.

• Selimut Tabung

Selimut tabung merupakan bidang yang menutupi bentuk tabung. Selimut tabung memiliki bentuk persegi panjang.

• Diamete

Apabila salah 1 alas/tutup yang berbentuk lingkaran dipotong di tengah-tengah menjadi ukuran yang sama maka jarak potongan tersebut adalah diameter tabung.

• Jari-jari

Jari-jari merupakan setengah dari diameter tabung.

Tabung memiliki 3 parameter ukuran yang bisa dihitung yaitu keliling, luas & volume.

Baca juga : Proposal: Tujuan, Struktur & Kaidah Bahasa

Rumus keliling tabung

Apabila kamu mempunyai sebuah kaleng & mau membuka kaleng tersebut dengan pisau maka pisau kamu akan mengiris bagian pinggir kaleng & mengelilingi pinggiran kaleng tersebut.

Hal inilah yang dinamakan dengan keliling alas/keliling tutup tabung. Kelililing alas tabung adalah jarak yang diperlukan untuk mengelilingi sebuah alas dari tabung.

Baca juga: Surat Pribadi: Pengertian, Struktur, Cara Membuat & Contohnya
Keliling alas tabung mempunyai rumus yang sama dengan lingkaran dimana rumusnya yaitu :

K= π x d

Keterangan :
K= keliling alas atau tutup
π= phi (22/7 atau 3,14)
d= diameter

Rumus luas permukaan tabung
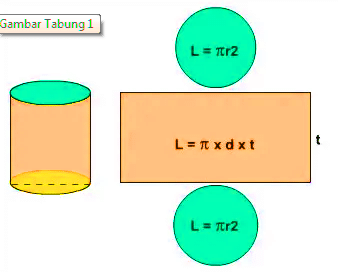
Sebuah tabung terdiri dari 3 bidang penyusun yaitu 2 buah lingkaran & selimut. Bidang penyusun tabung memiliki luasan yang berbeda dimana luas dari bidang penyusunnya yaitu:

Alas atau tutup = π x r2

Selimut = K x t

Luas permukaan dari tabung ialah 2 kali luas lingkarannya ditambah luas selimut atau:

Luas permukaan nya adalah= (2 x Luas Alas) + Luas Selimut

Keterangan :
K= keliling alas atau tutup
π= phi (22/7 atau 3,14)
r= jari-jari
t= tinggi tabung

Rumus volume Tabung
Jika sebuah tabung diisi air maka jumlah air yang dibutuhkan untuk mengisi tabung tersebut sampai penuh dinyatakan sebagai volume tabung.

Volume Tabung merupakan kapasitas ruang yang muat ditampung oleh tabung. Rumus volume tabung adalah :

V = Luas Alas x t

Keterangan :
V= volume tabung
t= tinggi tabung

Contoh soal yang berkaitan tabung
Sebuah tabung memiliki diameter 14 cm & tinggi 10 cm. Berapakah
Keliling alas tabung tersebut?
Luas permukaan tabung tersebut?
Volume tabung tersebut?
Jawaban nya:

Tabung mempunyai diameter 14 cm jadi jari-jarinya adalah 7cm

Keliling alas tabung

K= π x d = 22/7×14=44CM

Luas permukaan tabung

Untuk mengetahui luas permukaan diperlukan luas alas & luas selimut dimana :

Luas Alas = π x r2 = 22/7 x 72 = 154 cm2

Luas Selimut = K x t =44×10=440CM2

Jadi luas permukaan = (2 x Luas Alas) + Luas Selimut = (2 x 154) + 440 =308 + 440 = 748 cm2

Volume tabung

Volume = Luas Alas x t =154×10=1540CM3