Volume Segitiga Prisma lengkap dengan pengertian, penjelasan, rumus, dan cara menghitung soal nya beserta gambar segitiga prisma

Pada perhatiin ngga sih, kalau atap rumah kita sama tenda itu hampir mirip bentuknya? Jika diliat-liat lagi, bentuknya itu mirip 2 segitiga di tiap ujungnya, terus diselimuti dengan selimut yang berbentuk persegi panjang. Bentuk bangunan ini biasa juga disebut dengan bentuk prisma segitiga.
Disebut begitu karena alas & tutupnya tadi yang berbentuk segitiga. Dalam geometri, kita akan mempelajari pengertian & rumus prisma segitiga. Dalam kesempatan kali ini kita juga mau membahas berbagai contoh soalnya untuk bisa mengetahui materi ini secara lebih lanjut.
Prisma merupakan bangun ruang yang mempunyai tutup & alas dengan bentuk segi-n yang kongruen, sementara sisi tegaknya berbentuk persegi panjang.
Prisma merupakan bangun ruang yang terdiri dari atap & alas dengan bentuk segi-n yang kongruen beserta dipisahkan oleh sisi tegak berbentuk segi 4. Sisi atap & sisi alas prisma bersifat kongruen berarti ke2 sisi tersebut memiliki ukuran & bentuk yang sama. Bentuk sisi atap & sisi alas prisma berupa bangun datar segi-n, misalnya segi-3 yaitu (prisma segitiga) dan segi-4 yaitu (prisma segi empat:
Baca juga : Proposal: Tujuan, Struktur & Kaidah Bahasa
Sifat-Sifat Prisma
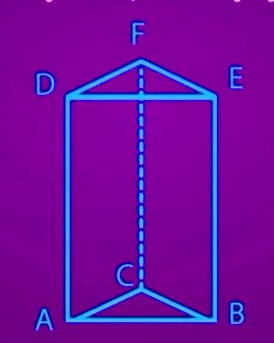
- Bentuk alas & atap prisma bersifat kongruen.
- Alas & atap prisma berbentuk segi-n, misalnya segi-3 & trapesium.
- Semua sisi tegak prisma berbentuk segi-4.
- Jumlah sisi prisma yaitu n+2, misalnya:
- Prisma segi 3 (n+2=3+2=5 sisi)
- Prisma segi 4 (n+2=4+2=6 sisi)
- Prisma segi 5 (n+2=5+2=7 sisi)
- Prisma segi 6 (n+2=6+2=8 sisi)
- Jumlah rusuk prisma yaitu 3n, misalnya:
- Prisma segi 3 (3×3 = 9 rusuk)
- Prisma segi 4 (4×3 = 12 rusuk)
- Prisma segi 5 (5×3 = 15 rusuk)
- Prisma segi 6 (6×3 = 18 rusuk)
- Jumlah titik sudut prisma yaitu 2n, misalnya:
- Prisma segi 3 (2×3 = 6 titik sudut)
- Prisma segi 4 (2×4 = 8 titik sudut)
- Prisma segi 5 (2×5 = 10 titik sudut)
- Prisma segi 6 = (2×6 = 12 titik sudut)
Rumus Prisma
t = tinggi prisma
La = luas alas
Nama Rumus
Volume (V) V = Luas alas × t
tinggi (t) jika diketahui V t = V ÷ Luas Alas
Luas Permukaan (L) L = t × ( a1 + a2 + … + an) + (2 × La)
L = t × (Keliling Alas)+(2×La)
Luas Prisma Segi-3 L = t × ( a1 + a2 + a3) + (2 × La)
Luas Prisma Segi-4 L = t × ( a1 + a2 + a3 + a4) + (2 × La)
Luas Prisma Segi-5 L = t × ( a1 + a2 + a3 + a4 + a5) + (2 × La)
Luas Prisma Segi-6 L = t × ( a1 + a2 + a3 + a4 + a5 + a6) + (2 × La)
Luas Alas (La) Disesuaikan dengan bentuk prisma
Cara Menghitung Volume Prisma
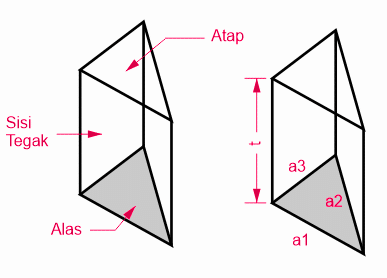
Hitunglah Volume Segitiga Prisma & luas permukaan prisma
Diketahui:
Prisma tersebut adalah prisma segi-3 dengan bentuk alas segi-3 siku-siku
t = 7 cm
- Alas Prisma berbentuk segi-3 siku-siku dengan masing-masing sisi tegak
a = 3 cm, bisa disebut alas segi-3
b = 4 cm, bisa disebut tinggi segi-3
Sehingga panjang sisi miring segi-3 siku-siku bisa dihitung memakai rumus Pythagoras
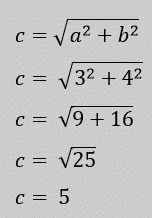
c = 5 cm, sebagai sisi miring segi-3
Ditanya:
Volume Prisma dan Luas Permukaan Prisma
Penyelesaian:
Volume Prisma
V = Luas alas × t
Karena alas prisma bentuknya segi-3, bisa dihitung
a = 3 cm, sebagai alas (a) & b = 4 cm sebagai tinggi (t)
La = ½ ×a×t
La = ½ ×3cm×4cm
La = 6 cm²
Jadi Volume Prisma
V = Luas alas × t
V = 6 cm² × 7 cm
V = 42 cm³
Luas Permukaan Prisma
Karena alas prisma berbentuk segi-3, sehingga bisa dihitung luas permukaan prisma dengan rumus
L = t × (a1+a2+a3)+(2×La)
Dari gambar bisa diketahui
Bisa diketahui masing-masing rusuk pada alasnya
a1= 5 cm
a2 =3 cm
a3 = 4 cm
Dengan t = 7 cm
Jadi luas alasnya
La = ½ ×a×t
La = ½ ×3cm×4CM
La = 6 CM²
Lalu bisa dihitung luas permukaan
L = t × (a1+a2+a3)+(2×La)
L = 7 cm × (5cm+3cm+4cm)+(2×6cm²)
L = 84 cm² + 12 cm²
L = 96 cm²
Jadi, volume prisma yaitu 42 cm³ & luas permukaan prisma 96 cm²